Contract Programmer Seeks Job in Cambridge (£500 reward)

Anyone in Cambridge need a programmer? I'll give you £500 if you can find me a job that I take.

CV at http://www.aspden.com

I make my usual promise, which I have paid out on several times:

If, within the next six months, I take a job which lasts longer than one month, and that is not obtained through an agency, then on the day the first cheque from that job cashes, I'll give £500 to the person who provided the crucial introduction.

If there are a number of people involved somehow, then I'll apportion it fairly between them. And if the timing conditions above are not quite met, or someone points me at a shorter contract which the £500 makes not worth taking, then I'll do something fair and proportional anyway.

And this offer applies even to personal friends, and to old contacts whom I have not got round to calling yet, and to people who are themselves offering work, because why wouldn't it?

And obviously if I find one through my own efforts then I'll keep the money. But my word is generally thought to be good, and I have made a public promise on my own blog to this effect, so if I cheat you you can blacken my name and ruin my reputation for honesty, which is worth much more to me than £500.

Clojure Setup from Scratch on a Clean Install of Debian 11

 
I've just installed Debian 11 on an ancient netbook whose hard disk failed, so that seems a chance to find out what
we need to do to make a functioning clojure environment from scratch.

The only changes I've made to my default install are things like getting sudo working and setting the UMASK, my home directory is brand new and empty.

first install clojure

$ sudo apt install clojure

$ clojure
Clojure 1.10.2
user=>

Latest stable according to clojure.org is 1.10.3, so that's really not bad!

and we've got a nice command-line REPL with bracket-balancing and history working

user=> (* 8 8)
64


Ctrl-D kills the REPL

Let's see if we can write a program:

$ cat > hello.clj
#!/usr/bin/env clojure
(println "hello")
^D

$ chmod + x hello.clj

$ ./hello.clj
"hello"


Startup time is quite long on my old netbook, so hello.clj takes 14 seconds to run, but the REPL, although sluggish to start up, actually runs pretty responsively once it has started.

And that's on a dell-mini, a 10 year old netbook that wasn't built for speed when it was new.

So that's a working installation, and you can use any editor to edit scripts and run them from the command line.

So far so good! Actually really impressed.

I can program like that, but I like to run clojure from within emacs, which is always the hard bit of getting any new language to work, so let's install emacs

$ sudo apt install emacs

and run it on our file

$ emacs hello.clj

We get no syntax highlighting, and the file is in 'fundamental mode', so emacs by default doesn't recognise .clj files

M-x package-list-packages

Shows some packages, but nothing clojure related, we need to add the melpa archive.

https://stable.melpa.org/#/getting-started

Suggests adding an incantation to your .emacs file:

So create the file ~/.emacs, and put:

(require 'package)
(add-to-list 'package-archives '("melpa-stable" . "https://stable.melpa.org/packages/") t)
(package-initialize)

 

in it.

Close emacs (Ctrl-X Ctrl-C) and restart it with:

$ emacs hello.clj

Now we can install clojure-mode

M-x package-refresh-contents

M-x package-install
clojure-mode
 

Again, close emacs and restart

$ emacs hello.clj

On restart, emacs recognises hello.clj as a clojure file, and syntax highlights it.


Again, this all works well so far. Adding MELPA to emacs is just one of those things you have to do in life.


But programming in clojure is best done with a running REPL, and for this we need CIDER

M-x package-install
cider

Once CIDER is installed, the hello.clj file has a CIDER menu, check that you've got CIDER 1.1.1
because all this stuff is still changing quite quickly, and it's a bit temperamental about version
numbers.

and there's an option to start a REPL

CIDER/Clojure/Start Clojure REPL

It complains 'are you sure you want to run cider-jack-in without a clojure project', which is exactly what I want to do, so I say yes.

I was so hoping this would work...

And it looks like it's doing something sensible, trying to start the system clojure with a command line, but it fails with an incomprehensible error message.

I think the problem is that it's trying to use the relatively new clojure command line tools to start a repl, which would be great, except that Debian hasn't got round to packaging them yet.

There doesn't seem to be a way to just use CIDER to edit and run a program using the system version of clojure.

(Although it does look like the CIDER people have at least tried to make that work, more power to them, and maybe it will work one day when the CLI tools get into debian)



So with a heavy heart, install leiningen and create a project file.

$ sudo apt install leiningen

$ cat > project.clj
(defproject vile "" :dependencies [ [org.clojure/clojure "1.10.2"] ])

and now try:

$ lein repl

That will then download a completely new version of clojure 1.10.2 into a local maven repository and
create a "target" directory full of crap in whatever directory you're in.

and eventually give you a repl

check it works, and then kill it with Ctrl-D

go back into emacs, and go into the hello.clj buffer, and again, try

CIDER/Clojure/Start Clojure REPL

Eventually, up should come a usable clojure REPL in emacs.

Now everything should be working, add (* 8 8) to hello.clj, and put the cursor in the middle of the
expression, and press C-M-x , and you should see the result of the evaluation => 64 display
conveniently in the buffer.

Also try M-. to go to the source code of a function, and M-, to go back to where you were

And there are lots of other lovely things about CIDER and using emacs and lisp together as they were meant to be used, which I will leave you to discover on your own.

Have fun!

-----------------------------------------------------------------------------------

Doing it the hard way:

CIDER's jack-in function is a bit magical for me, but luckily it will tell us what it's doing and which versions it needs:

The crucial line in the REPL startup text is:

;;  Startup: /usr/bin/lein update-in :dependencies conj \[nrepl/nrepl\ \"0.8.3\"\] -- update-in :plugins conj \[cider/cider-nrepl\ \"0.26.0\"\] -- repl :headless :host localhost

Which implies that we need [nrepl/nrepl "0.8.3"] as a dependency, and [cider/cider-nrepl "0.26.0"]
as a leiningen plugin, presumably to get leiningen to insert the cider-nrepl middleware to its nrepl
connection

So if we modify our project.clj file to look like:

(defproject vile ""
  :dependencies [ [org.clojure/clojure "1.10.2"]
                  [nrepl/nrepl "0.8.3"] ]
  :plugins      [ [cider/cider-nrepl "0.26.0"] ])

Then

$ lein repl

will start a command line REPL which also has a network port open with CIDER middleware attached,

and which you can connect to from CIDER with

M-x cider-connect

I prefer this way of doing things, for some reason. I think it feels a bit more solid and comprehensible than having emacs running my clojure process.

Fermat's Christmas Theorem : Fixed Points Come In Pairs

#!/usr/bin/env clojure

;; Fermats' Christmas Theorem: Fixed Points Come In Pairs

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;; Here's a bunch of code to make svg files of arrangements of coloured squares.
;; I'm using this to draw the windmills.
;; It's safe to ignore this if you're not interested in how to create such svg files.
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

(require 'clojure.xml)

(def squaresize 10)

(defn make-svg-rect [i j colour]
  {:tag :rect
   :attrs {:x (str (* i squaresize)) :y (str (* j squaresize)) :width  (str squaresize) :height (str squaresize)
           :style (str "fill:", colour, ";stroke:black;stroke-width:1px;stroke-linecap:butt;stroke-linejoin:miter;stroke-opacity:1")}})

(defn adjust-list [rectlist]
  (if (empty? rectlist) rectlist
      (let [hmin (apply min (map first  rectlist))
            vmax (apply max (map second rectlist))]
        (for [[a b c] rectlist] [(- a hmin) (- vmax b) c]))))

(defn make-svg [objects]
  {:tag :svg :attrs { :version "1.1"  :xmlns "http://www.w3.org/2000/svg"}
   :content (for [[i j c] (adjust-list objects)] (make-svg-rect i j c))})

(defn svg-file-from-rectlist [filename objects]
  (spit (str filename ".svg") (with-out-str (clojure.xml/emit (make-svg objects)))))

(defn hjoin
  ([sql1 sql2] (hjoin sql1 sql2 1))
  ([sql1 sql2 sep]
   (cond (empty? sql1) sql2
         (empty? sql2) sql1
         :else (let [xmax1 (apply max (map first sql1))
                     xmin2 (apply min (map first sql2))
                     shift  (+ 1 sep (- xmax1 xmin2))]
                 (concat sql1 (for [[h v c] sql2] [(+ shift h) v c]))))))

(defn hcombine [& sqllist] (reduce hjoin '() sqllist))

(defn svg-file [filename & objects]
  (svg-file-from-rectlist filename (apply hcombine objects)))

(defn orange [n] (if (< n 0) (range 0 n -1) (range 0 n 1)))

(defn make-composite-rectangle [h v hsquares vsquares colour]
  (for [i (orange hsquares) j (orange vsquares)] [(+ i h) (+ j v) colour]))

(defn make-windmill [[s p n]]
            (let [ s2 (quot s 2)
                  is2 (inc s2)
                  ds2 (- is2)]
              (concat (make-composite-rectangle  (- s2)  (- s2) s      s     "red")
                      (make-composite-rectangle  (- s2)  is2    p      n     "white")
                      (make-composite-rectangle  s2      ds2    (- p)  (- n) "white")
                      (make-composite-rectangle  ds2     (- s2) (- n)  p     "green")
                      (make-composite-rectangle  is2     s2     n      (- p) "green"))))

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;; end of drawing code
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;; and here's some code from the previous posts
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

;; code to tell us what number a triple represents
(defn total [[s p n]] (+ (* s s) (* 4 p n)))

;; the easy green transform
(defn green [[s p n]] [s n p])

;; and the complicated red transform, which doesn't look so bad once you've got it.
(defn red [[s p n]]
  (cond (< p (/ s 2))   [(- s (* 2 p))       (+ n (- s p)) p]
        (< (/ s 2) p s) [(- s (* 2 (- s p))) p (+ n (- s p))]
        (< s p (+ n s)) [(+ s (* 2 (- p s))) p (- n (- p s))]
        (< (+ n s) p)   [(+ s (* 2 n))       n (- p (+ n s))]
        :else [s p n]))

(defn make-thin-cross [n] [1 1 (/ (- n 1) 4)])

(defn victory [[s n p]]
  (assert (= n p))
  (hjoin
   (make-composite-rectangle 0 0 s s "red")
   (concat
    (make-composite-rectangle 0 0 n n "green")
    (make-composite-rectangle n n n n "green")
    (make-composite-rectangle 0 n n n "white")
    (make-composite-rectangle n 0 n n "white"))))

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;; end of code from previous posts
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;


;; A Christmas Eve Theorem

;; Fixed Points Come In Pairs



;; For any given number of squares, there are only so many ways of arranging them into windmills

;; In fact it's easy to enumerate them all

;; Any given number has only so many factors
(defn factors [n] (for [i (range 1 (inc n)) :when (zero? (rem n i))] i))

(factors 12) ; (1 2 3 4 6 12)
(factors 100) ; (1 2 4 5 10 20 25 50 100)

;; So it only has so many pairs of factors
(defn factor-pairs [n] (for [i (range 1 (inc n)) :when (zero? (rem n i))] [i (/ n i)]))

(factor-pairs 12) ; ([1 12] [2 6] [3 4] [4 3] [6 2] [12 1])
(factor-pairs 36) ; ([1 36] [2 18] [3 12] [4 9] [6 6] [9 4] [12 3] [18 2] [36 1])

;; And there are only so many odd numbers that square to less than a given number
(defn odd-numbers-whose-square-is-less-than[n] (for [i (range 1 n 2) :while (< (* i i) n)] i))

(odd-numbers-whose-square-is-less-than 49) ; (1 3 5) 
(odd-numbers-whose-square-is-less-than 103) ; (1 3 5 7 9)

;; given these functions we can just produce all the possible triples
(defn all-triples [m]
  (apply concat (for [s (odd-numbers-whose-square-is-less-than m)]
                  (for [[p n] (factor-pairs (/ (- m (* s s)) 4))]
                    [s p n]))))

(all-triples 5) ; ([1 1 1])
(all-triples 9) ; ([1 1 2] [1 2 1])
(all-triples 13) ; ([1 1 3] [1 3 1] [3 1 1])
(all-triples 49) ; ([1 1 12] [1 2 6] [1 3 4] [1 4 3] [1 6 2] [1 12 1] [3 1 10] [3 2 5] [3 5 2] [3 10 1] [5 1 6] [5 2 3] [5 3 2] [5 6 1])


;; And these triples come in three kinds

;; The first kind is triples that are fixed points of both the red and green transform

;; [1 1 1] is such a triple

(red [1 1 1]) ; [1 1 1]
(green [1 1 1]) ; [1 1 1]

;; It's not connected to any other triple. It is a red fixed point and a green fixed point simultaneously.

;; The second kind is triples that are fixed points of one transform, but not the other

;; [1 1 2] is such a triple

(red   [1 1 2]) ; [1 1 2]
(green [1 1 2]) ; [1 2 1]

;; It's connected to one other triple, by the green transform. Let's say it's got a green connection
;; which goes somewhere.

;; [1 2 1] is also such a triple

(red [1 2 1]) ; [1 2 1]
(green [1 2 1]) ; [1 1 2]

;; Its green connection goes to [1 1 2], to form a two-triple chain with two red fixedpoints on it.

;; [3 1 1] is also such a triple
(green [3 1 1]) ; [3 1 1]
(red [3 1 1]) ; [1 3 1]

;; but it's a fixed point of the green transform, so it has a red connection going out, which goes to [1 3 1]

;; The third kind of triple isn't a fixed point of either transform

;; [1 3 1] is such a triple

(red [1 3 1]) ; [3 1 1]
(green [1 3 1]) ; [1 1 3]

;; It has two connections out, one red and one green,
;; And they must go to two different triples, because the red transform changes the size of the red square
;; and the green one doesn't

;; Most triples are of this third kind, they can form links in chains

;; An even number of them can potentially form a loop

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

;; Suppose we start off from the first kind of triple.

;; We immediately find two fixed points, one red and one green, and we're done

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

;; Suppose we start off from the second kind of triple

;; It will have a link out

;; If we follow that link, then we can't go to a triple of the first kind, because that hasn't got any connections

;; If we go to a triple of the second kind, then we're done, because we'll use up its only
;; connection, and we've formed a complete chain with two fixed points

;; If we go to a triple of the third kind, then we have two triples, and one free connection out

;; Where can that connection go?

;; Not back into the chain we're making, all the connections of those triples are already accounted for.

;; So it must go to another triple and we're in the same situation.

;; We can never have more than one free connection on our chain

;; And we can't go on for ever, because there are only so many triples.

;; So eventually we have to link to another of the first kind of triple, having built a chain that connects
;; two fixed points.

;; A chain that connects two red or two green fixed points must have an odd number of connections
;; A chain that connects a red fixed point to a green fixed point must have an even number of connections

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

;; If we start from the third kind of triple, we've got two free connections, and we can attach triples to both of them.

;; But we never get more than two free connections.

;; We can't go on for ever, so we eventually either have to join our two free connections to make a loop, or we
;; have to be part of a chain which connects two fixed points of type 2

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

;; Christmas Eve Theorem

;; Fixed points come in pairs, if you start off from one and follow your links, you'll find another

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

;; This immediately implies Fermat's Christmas Theorem

;; Because for every number of the form 4n+1

;; We can make one, and only one thin cross, a red fixed point

;; The existence of this thin cross implies and is implied by the fact that the number is divisible by one.

;; It can't be part of a loop, by the argument above. And its chain can't go on for ever.

;; So if we follow the transforms, red, green, red, green, red, green ......

;; Sooner or later we'll hit another fixed point.

;; That other fixed point will be one of:

;; A square

;; A fat cross

;; or

;; A square-bladed windmill

;; If we find a square-bladed windmill, we've also found a way to write our number as the sum of an odd and an even square.

;; If we find a square, then we've shown that our number is itself an odd square

;; And if we find a fat cross, then we've shown that our number has a factorization, of the form s*(s+4n) for some n

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

;; Another way of saying that is that although this program is not generally safe to run on arbitrary triples:

(defn calculate-orbit
  ([triple transform] (calculate-orbit triple transform '()))
  ([triple transform orbit]
   (let [new (transform triple)]
     (if ( = new triple) (reverse (cons triple orbit))
         (recur new (if (= transform green) red green) (cons triple orbit))))))

;; Because it might go into an infinite loop, 


;; This program *is* safe to run, because starts at a red fixed point and so it must follow a chain and end at another fixed point
(defn christmas [n]
  (calculate-orbit (make-thin-cross n) green))

;; Let's try it out

(christmas 5) ; ([1 1 1])

(apply svg-file "windmills5-1" (map make-windmill (christmas 5)))



;; Here we show that 5 = 2*2 + 1*1

(christmas 9) ; ([1 1 2] [1 2 1])

(apply svg-file "windmills5-2" (map make-windmill (christmas 9))) ; nil




;; 9 = 3*3

(christmas 85) ; ([1 1 21] [1 21 1] [3 1 19] [3 19 1] [5 1 15] [5 15 1] [7 1 9] [7 9 1] [9 1 1])

(apply svg-file "windmills5-3" (map make-windmill (christmas 85)))




;; 85 = 9*9+2*2    (even though it's not prime!)

(christmas 201) ; ([1 1 50] [1 50 1] [3 1 48] [3 48 1] [5 1 44] [5 44 1] [7 1 38] [7 38 1] [9 1 30] [9 30 1] [11 1 20] [11 20 1] [13 1 8] [13 8 1] [3 8 6] [3 6 8] [9 6 5] [9 5 6] [1 5 10] [1 10 5] [11 5 4] [11 4 5] [3 12 4] [3 4 12] [5 4 11] [5 11 4] [13 4 2] [13 2 4] [9 15 2] [9 2 15] [5 22 2] [5 2 22] [1 25 2] [1 2 25] [3 2 24] [3 24 2] [7 2 19] [7 19 2] [11 2 10] [11 10 2] [9 10 3] [9 3 10] [3 16 3] [3 3 16])

(apply svg-file "windmills5-4" (map make-windmill (christmas 201)))



;; 201 = 3*(3 + 4*16) = 3*67

;; You might need to zoom in a bit on that last one, but the program will always work

;; Any number of the form 4n+1 can be either expressed as an odd square plus and even square, or it can be factored.

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

;;  Merry Christmas Everybody!

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

Christmas Theorem: Some Early Orbits

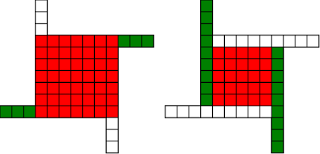
#!/usr/bin/env clojure

;; Fermats' Christmas Theorem: Some Early Orbits

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;; Here's a bunch of code to make svg files of arrangements of coloured squares.
;; I'm using this to draw the windmills.
;; It's safe to ignore this if you're not interested in how to create such svg files.
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

(require 'clojure.xml)

(def squaresize 10)

(defn make-svg-rect [i j colour]
  {:tag :rect
   :attrs {:x (str (* i squaresize)) :y (str (* j squaresize)) :width  (str squaresize) :height (str squaresize)
           :style (str "fill:", colour, ";stroke:black;stroke-width:1px;stroke-linecap:butt;stroke-linejoin:miter;stroke-opacity:1")}})

(defn adjust-list [rectlist]
  (if (empty? rectlist) rectlist
      (let [hmin (apply min (map first  rectlist))
            vmax (apply max (map second rectlist))]
        (for [[a b c] rectlist] [(- a hmin) (- vmax b) c]))))

(defn make-svg [objects]
  {:tag :svg :attrs { :version "1.1"  :xmlns "http://www.w3.org/2000/svg"}
   :content (for [[i j c] (adjust-list objects)] (make-svg-rect i j c))})

(defn svg-file-from-rectlist [filename objects]
  (spit (str filename ".svg") (with-out-str (clojure.xml/emit (make-svg objects)))))

(defn hjoin
  ([sql1 sql2] (hjoin sql1 sql2 1))
  ([sql1 sql2 sep]
   (cond (empty? sql1) sql2
         (empty? sql2) sql1
         :else (let [xmax1 (apply max (map first sql1))
                     xmin2 (apply min (map first sql2))
                     shift  (+ 1 sep (- xmax1 xmin2))]
                 (concat sql1 (for [[h v c] sql2] [(+ shift h) v c]))))))

(defn hcombine [& sqllist] (reduce hjoin '() sqllist))

(defn svg-file [filename & objects]
  (svg-file-from-rectlist filename (apply hcombine objects)))

(defn orange [n] (if (< n 0) (range 0 n -1) (range 0 n 1)))

(defn make-composite-rectangle [h v hsquares vsquares colour]
  (for [i (orange hsquares) j (orange vsquares)] [(+ i h) (+ j v) colour]))

(defn make-windmill [[s p n]]
            (let [ s2 (quot s 2)
                  is2 (inc s2)
                  ds2 (- is2)]
              (concat (make-composite-rectangle  (- s2)  (- s2) s      s     "red")
                      (make-composite-rectangle  (- s2)  is2    p      n     "white")
                      (make-composite-rectangle  s2      ds2    (- p)  (- n) "white")
                      (make-composite-rectangle  ds2     (- s2) (- n)  p     "green")
                      (make-composite-rectangle  is2     s2     n      (- p) "green"))))

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;; end of drawing code
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;; and here's some code from the previous posts
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

;; code to tell us what number a triple represents
(defn total [[s p n]] (+ (* s s) (* 4 p n)))

;; the easy green transform
(defn green [[s p n]] [s n p])

;; and the complicated red transform, which doesn't look so bad once you've got it.
(defn red [[s p n]]
  (cond (< p (/ s 2))   [(- s (* 2 p))       (+ n (- s p)) p]
        (< (/ s 2) p s) [(- s (* 2 (- s p))) p (+ n (- s p))]
        (< s p (+ n s)) [(+ s (* 2 (- p s))) p (- n (- p s))]
        (< (+ n s) p)   [(+ s (* 2 n))       n (- p (+ n s))]
        :else [s p n]))

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;; end of code from previous posts
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;


;; Let's start with the most simple candidate number, 5 = 4.1 + 1

;; We can always find a thin cross for any number of form 4n+1, almost by definition
(defn make-thin-cross [n] [1 1 (/ (- n 1) 4)])

(make-thin-cross 5) ; [1 1 1] 

;; [1 1 1] is in fact the only triple that can represent 5, can you see why?

(svg-file "windmills4-1" (make-windmill [1 1 1]))



;; This triple is a fixed point of the red transform (crosses always are)
(red   [1 1 1]) ; [1 1 1]

;; It's also a fixed point of the green transform (because n=p)
(green [1 1 1]) ; [1 1 1]

;; It's a fixed point of the green transform because its arms are squares, so I'll call it a square-bladed windmill

;; If we have a square-bladed windmill then we can transform it into an odd and an even square
(defn victory [[s n p]]
  (assert (= n p))
  (hjoin
   (make-composite-rectangle 0 0 s s "red")
   (concat
    (make-composite-rectangle 0 0 n n "green")
    (make-composite-rectangle n n n n "green")
    (make-composite-rectangle 0 n n n "white")
    (make-composite-rectangle n 0 n n "white"))))

(svg-file "windmills4-2" (victory [1 1 1]))



;; We see that 5 = 1*1 + 2*2


;; What about the next candidate number up, 9 = 4.2+1

(make-thin-cross 9) ; [1 1 2]

;; again, a red fixed point (because it's a cross)

(red [1 1 2]) ; [1 1 2]

;; But not a green one

(green [1 1 2]) ; [1 2 1]

;; however that is a fixed point of the red transform, so that's as far as we can go
(red [1 2 1]) ; [1 2 1]

;; If we look at this 'orbit' of the triple [1 1 2] as windmills, we see:

(apply svg-file "windmills4-3" (map make-windmill '([1 1 2] [1 2 1])))




;; We see a thin cross, a red fixed point, connected to a square, also a red fixed point

;; We've got two red fixed points connected by the green transform.

;; The square tells us that 9 has a factor, it's not a prime number


;; Let's do the next one

(make-thin-cross 13) ; [1 1 3]

(red [1 1 3]) ; [1 1 3]  ;; crosses are red fixed points

(green [1 1 3]) ; [1 3 1]

(red [1 3 1]) ; [3 1 1]

(green [3 1 1]) ; [3 1 1]

;; We've found a green fixed point, a square-bladed windmill

;; Our orbit is:
(apply svg-file "windmills4-4" (map make-windmill '([1 1 3] [1 3 1][3 1 1])))



;; We've got a red fixed point, connected by a green step and then a red step to a green fixed point

(svg-file "windmills4-5" (victory [3 1 1]))



;; The green fixed point gives us our decomposition into odd and even squares

;; 13 = 3*3 + 2*2

;; The Christmas theorem is looking good so far....

(make-thin-cross 17) ; [1 1 4] ;; cross

(green [1 1 4]) ; [1 4 1]

(red [1 4 1]) ; [3 1 2]

(green [3 1 2]) ; [3 2 1]

(red [3 2 1]) ; [1 2 2]

(green [1 2 2]) ; [1 2 2]  ;; square blades!

;; Our orbit is:
(apply svg-file "windmills4-6" (map make-windmill '([1 1 4] [1 4 1][3 1 2] [3 2 1] [1 2 2])))



;; A red fixed point connected to a green fixed point by four steps. green,red,green,red

(svg-file "windmills4-7" (victory [1 2 2]))



;; 17 = 1*1 + 4*4



(make-thin-cross 21) ; [1 1 5]

(green [1 1 5]) ; [1 5 1]

(red [1 5 1]) ; [3 1 3]

(green [3 1 3]) ; [3 3 1]

(red [3 3 1]) ; [3 3 1]

;; Our orbit is:
(apply svg-file "windmills4-8" (map make-windmill '([1 1 5] [1 5 1][3 1 3] [3 3 1])))



;; A red fixed point connected to a red fixed point by three steps. green,red,green

;; The red fixed point is a cross. Because the red square is not 1x1, I'm going to call that a 'fat cross'

;; If we have a fat cross, that tells us that our number has a factorization

;; Look:

(svg-file "windmills4-9"
       (concat
        (make-composite-rectangle 0 0 3 3 "red")
        (make-composite-rectangle 3 0 1 3 "green")
        (make-composite-rectangle 4 0 1 3 "white")
        (make-composite-rectangle 5 0 1 3 "green")
        (make-composite-rectangle 6 0 1 3 "white")))



;; In fact, it tells us that 21 = 3*(3+4) = 3*7

;; The pattern here is that our initial thin crosses (red fixed points) are always connected to other fixed points

;; If the other fixed point is green, it shows us that we have an odd and even square that represent our number

;; If the other fixed point is red, then it shows us that our number has a factor, i.e that it isn't prime.

;; That's the Christmas Theorem.

;; Why would it be true???

Chrismas Theorem: Automatic Windmills

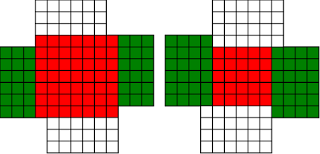
#!/usr/bin/env clojure

;; Fermats' Christmas Theorem: Automatic Windmills

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;; Here's a bunch of code to make svg files of arrangements of coloured squares.
;; I'm using this to draw the windmills.
;; It's safe to ignore this if you're not interested in how to create such svg files.
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

(require 'clojure.xml)

(def squaresize 10)

(defn make-svg-rect [i j colour]
  {:tag :rect
   :attrs {:x (str (* i squaresize)) :y (str (* j squaresize)) :width  (str squaresize) :height (str squaresize)
           :style (str "fill:", colour, ";stroke:black;stroke-width:1px;stroke-linecap:butt;stroke-linejoin:miter;stroke-opacity:1")}})

(defn adjust-list [rectlist]
  (if (empty? rectlist) rectlist
      (let [hmin (apply min (map first  rectlist))
            vmax (apply max (map second rectlist))]
        (for [[a b c] rectlist] [(- a hmin) (- vmax b) c]))))

(defn make-svg [objects]
  {:tag :svg :attrs { :version "1.1"  :xmlns "http://www.w3.org/2000/svg"}
   :content (for [[i j c] (adjust-list objects)] (make-svg-rect i j c))})

(defn svg-file-from-rectlist [filename objects]
  (spit (str filename ".svg") (with-out-str (clojure.xml/emit (make-svg objects)))))

(defn hjoin
  ([sql1 sql2] (hjoin sql1 sql2 1))
  ([sql1 sql2 sep]
   (cond (empty? sql1) sql2
         (empty? sql2) sql1
         :else (let [xmax1 (apply max (map first sql1))
                     xmin2 (apply min (map first sql2))
                     shift  (+ 1 sep (- xmax1 xmin2))]
                 (concat sql1 (for [[h v c] sql2] [(+ shift h) v c]))))))

(defn hcombine [& sqllist] (reduce hjoin '() sqllist))

(defn svg-file [filename & objects]
  (svg-file-from-rectlist filename (apply hcombine objects)))

(defn orange [n] (if (< n 0) (range 0 n -1) (range 0 n 1)))

(defn make-composite-rectangle [h v hsquares vsquares colour]
  (for [i (orange hsquares) j (orange vsquares)] [(+ i h) (+ j v) colour]))

(defn make-windmill [[s p n]]
            (let [ s2 (quot s 2)
                  is2 (inc s2)
                  ds2 (- is2)]
              (concat (make-composite-rectangle  (- s2)  (- s2) s      s     "red")
                      (make-composite-rectangle  (- s2)  is2    p      n     "white")
                      (make-composite-rectangle  s2      ds2    (- p)  (- n) "white")
                      (make-composite-rectangle  ds2     (- s2) (- n)  p     "green")
                      (make-composite-rectangle  is2     s2     n      (- p) "green"))))

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;; end of drawing code
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;


;; So far so good, but the red transform is a bit manual for my taste. It's easy to see how to do it
;; by eye, but I want to automate that.

;; Let's go over our sequence of shapes for 37 again
(svg-file "windmills3-1" (make-windmill [1 1 9]) (make-windmill [1 9 1]) (make-windmill [3 1 7])(make-windmill [3 7 1])(make-windmill [5 1 3])(make-windmill [5 3 1])(make-windmill [1 3 3]))




;; The red transform has a way of flipping the shapes and exchanging the white and green colours, which I'm going to ignore.

;; There may be a more principled way of drawing the triples so that the associated windmills are
;; more consistent with each other, but I don't want to get distracted. I'm already deep down one
;; rabbit hole, and so I'm going to avoid this branch tunnel, or at least save it for later.

;; So, automating the red transform:

;; By eye it's always obvious what to do, but it's not so obvious to a computer,

;; There are actually six different cases to consider, depending on the relative sizes of s, n and p!

;; Let's fix s to be seven, and n to be three, and let p vary, that should be enough to capture all the different cases

;; Start off with p as one, the smallest it can be

;; The picture for the transformation we want to do is:
(svg-file "windmills3-2" (make-windmill [7 1 3]) (make-windmill [5 9 1]))




;; We see that the arms of the windmill are all extending into the square, taking squares until they
;; collide with the other arms.

;; Because the arms stay n wide throughout, the collision happens when the arms have all extended by s-n squares.

;; So the normal length 3 gets 6 (7-1) added to it, to become 9, the parallel length 1 stays the same

;; And the red square loses the parallel length taken off it on both sides, so s=7 becomes s=7-2*1

;; We might think that the transformation would take [7 1 3] to [5 1 9]

;; Or in general terms, s -> s-2p n->n+(s-p), p->p

(svg-file "windmills3-3" (make-windmill [7 1 3]) (make-windmill [5 1 9]))



;; But no! During the transformation, the arm that started at the north-west corner extended down so that it's now the arm that
;; starts at the south-west corner, so we need to make our triple with 1 as the normal length and 9 as the parallel length

;; That's what causes the red-green colour flip in our drawings

;; So in fact what we want is s -> s-2p p->n+(s-p), n->p

(svg-file "windmills3-4" (make-windmill [7 1 3]) (make-windmill [5 9 1]))




;; In order for this procedure to work, we need s-2p to be positive, or equivalently p < s/2

;; In code:
(defn red [[s p n]]
  (cond (< p (/ s 2)) [(- s (* 2 p)) (+ n (- s p)) p]
        :else [s p n]))

;; If the condition's not true, we'll just hand back the original triple (for now...)

(red [7 1 3]) ; [5 9 1]

(let [[s p n][7 1 3]] (svg-file "windmills3-5" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; So now let's increase p by one
(let [[s p n][7 2 3]] (svg-file "windmills3-6" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; Looks good, and again
(let [[s p n][7 3 3]] (svg-file "windmills3-7" (make-windmill [s p n]) (make-windmill (red [s p n]))))




;; but increasing p again
(let [[s p n][7 4 3]] (svg-file "windmills3-8" (make-windmill [s p n]) (make-windmill (red [s p n]))))




;; we see that our idea has failed, that transformation would take up more squares than we have (p >  s/2)
;; So we've just given up and returned the original triple

;; Notice that we haven't seen the case where p=s/2, because s is odd, so s/2 isn't an integer

;; If p> s/2, we can do roughly the same thing, but we have to stop earlier.

;; If we imagine our arms extending in, then we'll see that they have to stop after three moves, when they collide with each other
;; that three comes from s-p, so the normal length needs to extend by s-p, and the square needs to lose s-p from both sides
;; And in this case, we don't need to swap n and p, the normal length remains the normal length.

;; The condition for being able to do this is that s-p is positive, or s>p

;; And the transformation is s->s-2(s-p), n->n+(s-p), p->p

;; Adding this case to our transform
(defn red [[s p n]]
  (cond (< p (/ s 2))   [(- s (* 2 p))       (+ n (- s p)) p]
        (< (/ s 2) p s) [(- s (* 2 (- s p))) p (+ n (- s p))]
        :else [s p n]))

(red [7 4 3]) ; [1 4 6]

(let [[s p n][7 4 3]] (svg-file "windmills3-9" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; In this case, our drawing appears to flip, because the corners of the red square have moved!
;; But we can see that the shape is the same, and the number of squares is the same.

;; keep increasing p
(let [[s p n][7 5 3]] (svg-file "windmills3-10" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; again it works

;; keep increasing p
(let [[s p n][7 6 3]] (svg-file "windmills3-11" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; and again
(let [[s p n][7 7 3]] (svg-file "windmills3-12" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; this time p=s, and so our procedure does nothing.

;; In fact, there's nothing we can do here, we can neither shrink nor expand the red square while keeping the shape the same.

;; I'm going to call this special, more symmetric type of windmill a 'cross'. It's a fixed point of our red
;; transform, we just let it return the same triple.

;; What if we make p even bigger?
(let [[s p n][7 8 3]] (svg-file "windmills3-13" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; Neither of our previous ideas will work, but there's a new option here, we can make the square bigger at the expense of the arms
(svg-file "windmills3-14" (make-windmill [7 8 3]) (make-windmill [9 8 2]))



;; Again, the shape appears to flip, but it's just a mirror image of the shape we would get if we extended the red square

;; so how do we code this case?

;; Well, the red square can get bigger (on both sides), by the amount by which the parallel length exceeds the square
;; i.e. p-s
;; The parallel length stays the same, and the normal length goes down by p-s

;; so s-> s+2*(p-s), p->p, n-> n-(p-s)
;; And this should work as long as p-s<n, or p<n+s



(defn red [[s p n]]
  (cond (< p (/ s 2))   [(- s (* 2 p))       (+ n (- s p)) p]
        (< (/ s 2) p s) [(- s (* 2 (- s p))) p (+ n (- s p))]
        (< s p (+ n s)) [(+ s (* 2 (- p s))) p (- n (- p s))]
        :else [s p n]))

(red [7 8 3]) ; [9 8 2]

(let [[s p n][7 8 3]] (svg-file "windmills3-15" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; increase p
(let [[s p n][7 9 3]] (svg-file "windmills3-16" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; looks good

;; increase p
(let [[s p n][7 10 3]] (svg-file "windmills3-17" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; Now p=s+n, and we can't make any of our previous ideas work.

;; We could increase the red square to fill the whole shape now, but the result wouldn't be a windmill, and there's nothing
;; else we can do, so we'll leave this case as a fixed point.

;; I'll call this special symmetric windmill a 'square', for obvious reasons.

;; what if p is even larger than s+n?

(let [[s p n][7 11 3]] (svg-file "windmills3-18" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; now there is something we can do, we can increase size of the square by n
;; this takes s+n squares from the parallel length

(svg-file "windmills3-19" (make-windmill [7 11 3]) (make-windmill [13 3 1]))



;; Again we need to swap normal and parallel

;; So our final transformation is

;; s-> s+2n, p->n, n-> p-(s+n)
;; And this is the final case, it will work whenever p > n+s

(defn red [[s p n]]
  (cond (< p (/ s 2))   [(- s (* 2 p))       (+ n (- s p)) p]
        (< (/ s 2) p s) [(- s (* 2 (- s p))) p (+ n (- s p))]
        (< s p (+ n s)) [(+ s (* 2 (- p s))) p (- n (- p s))]
        (< (+ n s) p)   [(+ s (* 2 n))       n (- p (+ n s))]
        :else [s p n]))


(let [[s p n][7 11 3]] (svg-file "windmills3-20" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; increase p
(let [[s p n][7 12 3]] (svg-file "windmills3-21" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; increase p 
(let [[s p n][7 13 3]] (svg-file "windmills3-22" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; increase p 
(let [[s p n][7 14 3]] (svg-file "windmills3-23" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; And we're done, this will work however large p is!

;; That was very fiddly and took me several goes and a bit of paper to get right. But it correctly captures the four different cases that
;; are so easy to do by eye, and also the two cases where it fails, the squares and crosses.