Chrismas Theorem: Automatic Windmills

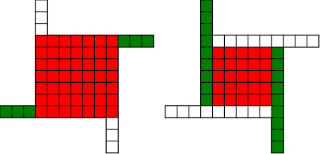
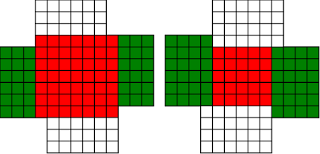
#!/usr/bin/env clojure

;; Fermats' Christmas Theorem: Automatic Windmills

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;; Here's a bunch of code to make svg files of arrangements of coloured squares.
;; I'm using this to draw the windmills.
;; It's safe to ignore this if you're not interested in how to create such svg files.
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

(require 'clojure.xml)

(def squaresize 10)

(defn make-svg-rect [i j colour]
  {:tag :rect
   :attrs {:x (str (* i squaresize)) :y (str (* j squaresize)) :width  (str squaresize) :height (str squaresize)
           :style (str "fill:", colour, ";stroke:black;stroke-width:1px;stroke-linecap:butt;stroke-linejoin:miter;stroke-opacity:1")}})

(defn adjust-list [rectlist]
  (if (empty? rectlist) rectlist
      (let [hmin (apply min (map first  rectlist))
            vmax (apply max (map second rectlist))]
        (for [[a b c] rectlist] [(- a hmin) (- vmax b) c]))))

(defn make-svg [objects]
  {:tag :svg :attrs { :version "1.1"  :xmlns "http://www.w3.org/2000/svg"}
   :content (for [[i j c] (adjust-list objects)] (make-svg-rect i j c))})

(defn svg-file-from-rectlist [filename objects]
  (spit (str filename ".svg") (with-out-str (clojure.xml/emit (make-svg objects)))))

(defn hjoin
  ([sql1 sql2] (hjoin sql1 sql2 1))
  ([sql1 sql2 sep]
   (cond (empty? sql1) sql2
         (empty? sql2) sql1
         :else (let [xmax1 (apply max (map first sql1))
                     xmin2 (apply min (map first sql2))
                     shift  (+ 1 sep (- xmax1 xmin2))]
                 (concat sql1 (for [[h v c] sql2] [(+ shift h) v c]))))))

(defn hcombine [& sqllist] (reduce hjoin '() sqllist))

(defn svg-file [filename & objects]
  (svg-file-from-rectlist filename (apply hcombine objects)))

(defn orange [n] (if (< n 0) (range 0 n -1) (range 0 n 1)))

(defn make-composite-rectangle [h v hsquares vsquares colour]
  (for [i (orange hsquares) j (orange vsquares)] [(+ i h) (+ j v) colour]))

(defn make-windmill [[s p n]]
            (let [ s2 (quot s 2)
                  is2 (inc s2)
                  ds2 (- is2)]
              (concat (make-composite-rectangle  (- s2)  (- s2) s      s     "red")
                      (make-composite-rectangle  (- s2)  is2    p      n     "white")
                      (make-composite-rectangle  s2      ds2    (- p)  (- n) "white")
                      (make-composite-rectangle  ds2     (- s2) (- n)  p     "green")
                      (make-composite-rectangle  is2     s2     n      (- p) "green"))))

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;; end of drawing code
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;


;; So far so good, but the red transform is a bit manual for my taste. It's easy to see how to do it
;; by eye, but I want to automate that.

;; Let's go over our sequence of shapes for 37 again
(svg-file "windmills3-1" (make-windmill [1 1 9]) (make-windmill [1 9 1]) (make-windmill [3 1 7])(make-windmill [3 7 1])(make-windmill [5 1 3])(make-windmill [5 3 1])(make-windmill [1 3 3]))




;; The red transform has a way of flipping the shapes and exchanging the white and green colours, which I'm going to ignore.

;; There may be a more principled way of drawing the triples so that the associated windmills are
;; more consistent with each other, but I don't want to get distracted. I'm already deep down one
;; rabbit hole, and so I'm going to avoid this branch tunnel, or at least save it for later.

;; So, automating the red transform:

;; By eye it's always obvious what to do, but it's not so obvious to a computer,

;; There are actually six different cases to consider, depending on the relative sizes of s, n and p!

;; Let's fix s to be seven, and n to be three, and let p vary, that should be enough to capture all the different cases

;; Start off with p as one, the smallest it can be

;; The picture for the transformation we want to do is:
(svg-file "windmills3-2" (make-windmill [7 1 3]) (make-windmill [5 9 1]))




;; We see that the arms of the windmill are all extending into the square, taking squares until they
;; collide with the other arms.

;; Because the arms stay n wide throughout, the collision happens when the arms have all extended by s-n squares.

;; So the normal length 3 gets 6 (7-1) added to it, to become 9, the parallel length 1 stays the same

;; And the red square loses the parallel length taken off it on both sides, so s=7 becomes s=7-2*1

;; We might think that the transformation would take [7 1 3] to [5 1 9]

;; Or in general terms, s -> s-2p n->n+(s-p), p->p

(svg-file "windmills3-3" (make-windmill [7 1 3]) (make-windmill [5 1 9]))



;; But no! During the transformation, the arm that started at the north-west corner extended down so that it's now the arm that
;; starts at the south-west corner, so we need to make our triple with 1 as the normal length and 9 as the parallel length

;; That's what causes the red-green colour flip in our drawings

;; So in fact what we want is s -> s-2p p->n+(s-p), n->p

(svg-file "windmills3-4" (make-windmill [7 1 3]) (make-windmill [5 9 1]))




;; In order for this procedure to work, we need s-2p to be positive, or equivalently p < s/2

;; In code:
(defn red [[s p n]]
  (cond (< p (/ s 2)) [(- s (* 2 p)) (+ n (- s p)) p]
        :else [s p n]))

;; If the condition's not true, we'll just hand back the original triple (for now...)

(red [7 1 3]) ; [5 9 1]

(let [[s p n][7 1 3]] (svg-file "windmills3-5" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; So now let's increase p by one
(let [[s p n][7 2 3]] (svg-file "windmills3-6" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; Looks good, and again
(let [[s p n][7 3 3]] (svg-file "windmills3-7" (make-windmill [s p n]) (make-windmill (red [s p n]))))




;; but increasing p again
(let [[s p n][7 4 3]] (svg-file "windmills3-8" (make-windmill [s p n]) (make-windmill (red [s p n]))))




;; we see that our idea has failed, that transformation would take up more squares than we have (p >  s/2)
;; So we've just given up and returned the original triple

;; Notice that we haven't seen the case where p=s/2, because s is odd, so s/2 isn't an integer

;; If p> s/2, we can do roughly the same thing, but we have to stop earlier.

;; If we imagine our arms extending in, then we'll see that they have to stop after three moves, when they collide with each other
;; that three comes from s-p, so the normal length needs to extend by s-p, and the square needs to lose s-p from both sides
;; And in this case, we don't need to swap n and p, the normal length remains the normal length.

;; The condition for being able to do this is that s-p is positive, or s>p

;; And the transformation is s->s-2(s-p), n->n+(s-p), p->p

;; Adding this case to our transform
(defn red [[s p n]]
  (cond (< p (/ s 2))   [(- s (* 2 p))       (+ n (- s p)) p]
        (< (/ s 2) p s) [(- s (* 2 (- s p))) p (+ n (- s p))]
        :else [s p n]))

(red [7 4 3]) ; [1 4 6]

(let [[s p n][7 4 3]] (svg-file "windmills3-9" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; In this case, our drawing appears to flip, because the corners of the red square have moved!
;; But we can see that the shape is the same, and the number of squares is the same.

;; keep increasing p
(let [[s p n][7 5 3]] (svg-file "windmills3-10" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; again it works

;; keep increasing p
(let [[s p n][7 6 3]] (svg-file "windmills3-11" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; and again
(let [[s p n][7 7 3]] (svg-file "windmills3-12" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; this time p=s, and so our procedure does nothing.

;; In fact, there's nothing we can do here, we can neither shrink nor expand the red square while keeping the shape the same.

;; I'm going to call this special, more symmetric type of windmill a 'cross'. It's a fixed point of our red
;; transform, we just let it return the same triple.

;; What if we make p even bigger?
(let [[s p n][7 8 3]] (svg-file "windmills3-13" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; Neither of our previous ideas will work, but there's a new option here, we can make the square bigger at the expense of the arms
(svg-file "windmills3-14" (make-windmill [7 8 3]) (make-windmill [9 8 2]))



;; Again, the shape appears to flip, but it's just a mirror image of the shape we would get if we extended the red square

;; so how do we code this case?

;; Well, the red square can get bigger (on both sides), by the amount by which the parallel length exceeds the square
;; i.e. p-s
;; The parallel length stays the same, and the normal length goes down by p-s

;; so s-> s+2*(p-s), p->p, n-> n-(p-s)
;; And this should work as long as p-s<n, or p<n+s



(defn red [[s p n]]
  (cond (< p (/ s 2))   [(- s (* 2 p))       (+ n (- s p)) p]
        (< (/ s 2) p s) [(- s (* 2 (- s p))) p (+ n (- s p))]
        (< s p (+ n s)) [(+ s (* 2 (- p s))) p (- n (- p s))]
        :else [s p n]))

(red [7 8 3]) ; [9 8 2]

(let [[s p n][7 8 3]] (svg-file "windmills3-15" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; increase p
(let [[s p n][7 9 3]] (svg-file "windmills3-16" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; looks good

;; increase p
(let [[s p n][7 10 3]] (svg-file "windmills3-17" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; Now p=s+n, and we can't make any of our previous ideas work.

;; We could increase the red square to fill the whole shape now, but the result wouldn't be a windmill, and there's nothing
;; else we can do, so we'll leave this case as a fixed point.

;; I'll call this special symmetric windmill a 'square', for obvious reasons.

;; what if p is even larger than s+n?

(let [[s p n][7 11 3]] (svg-file "windmills3-18" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; now there is something we can do, we can increase size of the square by n
;; this takes s+n squares from the parallel length

(svg-file "windmills3-19" (make-windmill [7 11 3]) (make-windmill [13 3 1]))



;; Again we need to swap normal and parallel

;; So our final transformation is

;; s-> s+2n, p->n, n-> p-(s+n)
;; And this is the final case, it will work whenever p > n+s

(defn red [[s p n]]
  (cond (< p (/ s 2))   [(- s (* 2 p))       (+ n (- s p)) p]
        (< (/ s 2) p s) [(- s (* 2 (- s p))) p (+ n (- s p))]
        (< s p (+ n s)) [(+ s (* 2 (- p s))) p (- n (- p s))]
        (< (+ n s) p)   [(+ s (* 2 n))       n (- p (+ n s))]
        :else [s p n]))


(let [[s p n][7 11 3]] (svg-file "windmills3-20" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; increase p
(let [[s p n][7 12 3]] (svg-file "windmills3-21" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; increase p 
(let [[s p n][7 13 3]] (svg-file "windmills3-22" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; increase p 
(let [[s p n][7 14 3]] (svg-file "windmills3-23" (make-windmill [s p n]) (make-windmill (red [s p n]))))



;; And we're done, this will work however large p is!

;; That was very fiddly and took me several goes and a bit of paper to get right. But it correctly captures the four different cases that
;; are so easy to do by eye, and also the two cases where it fails, the squares and crosses.